O problema cu ariile unor patrate

In timp ce statea la coada la spital si se holba la placile de faianta din fatza lui, Gramo s-a gandit la asta. Sa ne inchipuim ca am avea niste patrate aranjate in felul urmator:


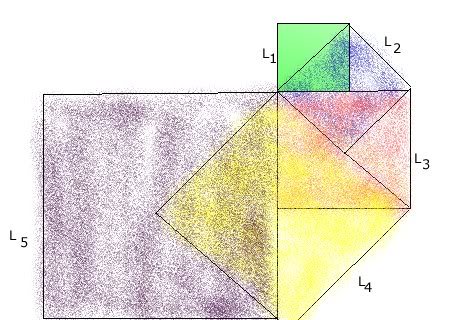
Primul patrat are latura L1, al doilea are ca latura diagonala primului patrat (L2) s.a.m.d.

Daca primul patrat are latura de marimea 1, aria lui e 1. L2 este radical din 1^2 + 1^2, adica radical din 2. Aria celui de-al doilea patrat e radical din 2 x radical din doi, adica 2.

Diagonala celui de-al doilea patrat (adica L3) e radical din (2 x radical din 2^2), adica radical din 4. Deci aria celui de-al treilea patrat e 4. Iar aria celui de al patrulea patrat pare sa fie 8 s.a.m.d.

Dar care e relatia intre ariile patratelor alora, indiferent de marimea laturii primului patrat? Eh? Spit it out! 🙂

p.s. La intrebarea asta Gramo a gasit un raspuns, dar n-a apucat sa il verifice. Toata povestea s-a petrecut spontan si nu aveam acces la net 🙂 After all, nici nu e mare lucru. E probabil o problema banala. Dar uneori e funny sa te gandesti la chestii banale 🙂

6 thoughts on “O problema cu ariile unor patrate”

  2. gramos

    cred ca da 🙂

    iar din ce spui tu reiese ca:
    An = 2^n-1 x L1^2

    iar in ce priveste raportul dintre arii (fiindca asta ma interesa), reiese ca:
    An= 2 x An-1

    adica de la un patrat la altul aria se dubleaza; iar chestia asta o poti gasi uitandu-te la numere si calculand, dar si vizual, fara nici un fel de calcul:

    daca iti inchipui ca patratul verde e format din doua triunghiuri si il iei pe cel din dreapta-sus si il rotesti si il pui in al doilea patrat, vezi ca ai folosit primul patrat pentru a acoperi jumatate din patratul al doilea;

    iar dupa aia vezi ca poti repeta chestia cu al doilea patrat s.a.m.d.

    p.s. ok, chestia cu “n-a apucat sa verifice” a fost probabil un pic trasa de par, dar am zis ca poate vrea si altcineva sa se amuze cu patratele alea, inainte sa primeasca solutia pe tava 🙂

  3. fractalcapone

    hmmm… cred ca o sa caut cate ceva infoz despre fractali…
    momentan imi pare ca e un fractal “uratzel”, un fel de var indepartat si mai dumb al familiei mandelbrot.
    poate aflu si “cum poate fi infrumusetat un fractal uratzel” 🙂

    ps: oricum, jocul cu patratelele chiar e funny 🙂

  4. gramos

    @fractalcapone: pentru ceva care sa semene cu un fractal m-am gandit la constructia inversa: pornesti cu un patrat mare si obtii patrate tot mai mici, la nesfarsit;

    latura patratului mare devine diagonala patratului mai mic; cand inaintezi de la un patrat mai mare la un patrat mai mic poti sa alegi care latura sa o folosesti – probabil in functie de asta forma rezultata o sa fie mai cute sa nu 🙂

    uite o imagine aici; ceea ce iese seamana cu un fractal, dar nu stiu daca chiar e asa ceva 🙂

Comments are closed.